When it comes to the world of mathematics, questions often arise that challenge our understanding and provoke thought. One such question is: is 0 an even number? On the surface, it might seem straightforward, but for many, it sparks curiosity and debate. Understanding the nature of numbers and their classifications is crucial, especially when it involves a number as unique as zero.
Zero holds a unique place in the world of numbers. It is neither positive nor negative, serving as a critical placeholder in our number system. The concept of even and odd numbers is one of the fundamental aspects of number theory. Even numbers are those divisible by two without any remainder, and zero fits this definition perfectly. Yet, the question remains prevalent in discussions both in classrooms and online forums.
In this article, we will delve into the intricacies of why zero is considered an even number. We will analyze its properties, explore mathematical theories, and address common misconceptions. By the end of this discussion, you will have a comprehensive understanding of the topic, backed by mathematical evidence and logical reasoning. So, let’s begin our exploration into the fascinating realm of numbers and clarify once and for all, is 0 truly an even number?
Read also:Philanthropy Gala Red Carpet A Night Of Glamour And Giving
Table of Contents
- Definition of Even Numbers
- Mathematical Properties of Zero
- Is 0 an Even Number?
- Historical Perspective on Zero
- Real-World Applications of Zero
- Common Misconceptions About Zero
- Zero and the Number Line
- Teaching Zero as an Even Number
- How Does Zero Affect Computations?
- Zero in Different Mathematical Systems
- Why Does It Matter if 0 Is Even?
- Zero in Popular Culture
- Frequently Asked Questions
- Conclusion
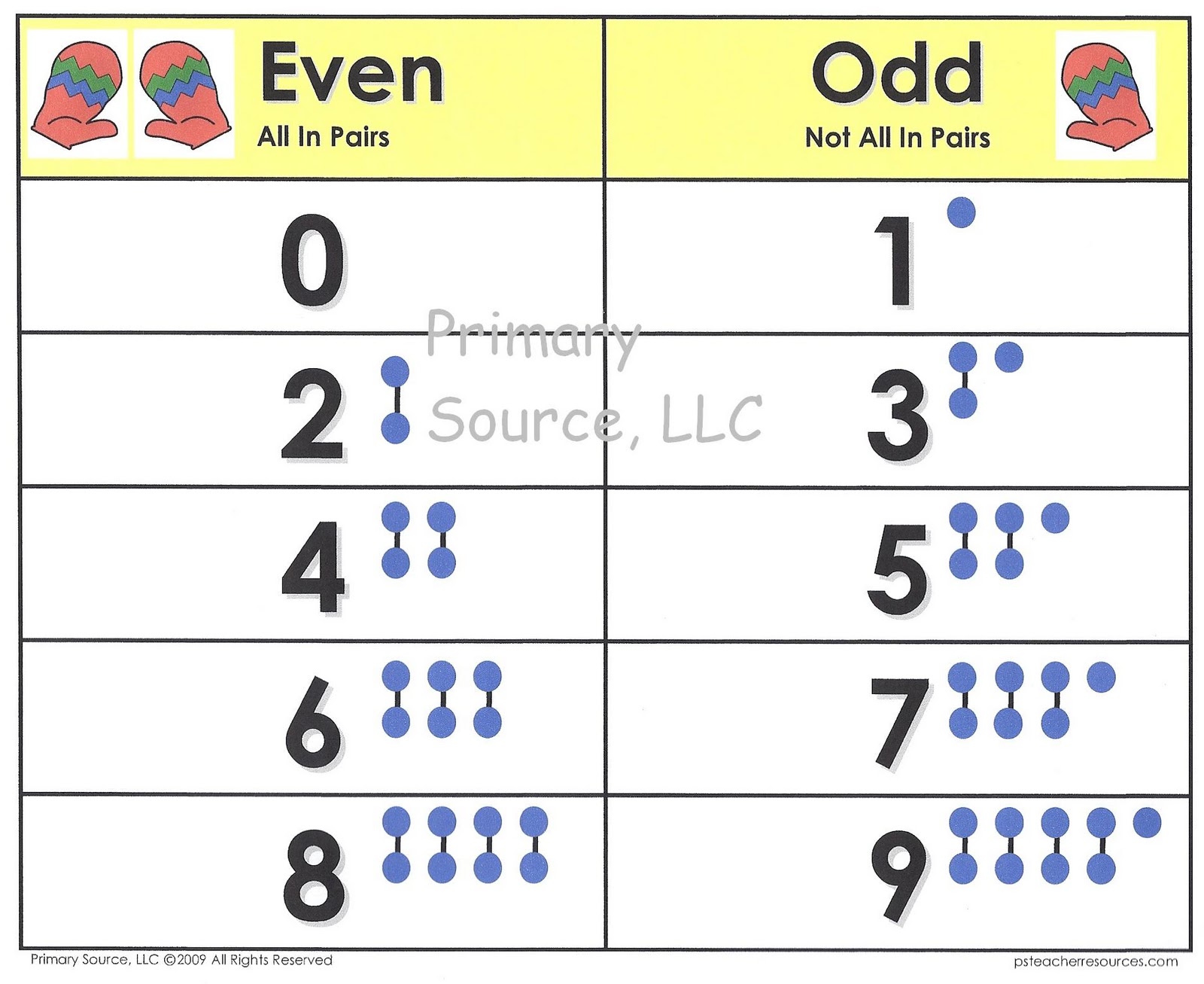
Definition of Even Numbers
Even numbers are integral elements in mathematics, characterized by their divisibility by two. In simpler terms, when an even number is divided by two, the result is a whole number with no remainder. This definition holds true across all number systems and has been a cornerstone of arithmetic for centuries.
One of the simplest examples of even numbers includes 2, 4, 6, 8, and so on. Each of these numbers can be divided by two to yield another integer. This fundamental property of evenness is essential in various mathematical operations and forms the basis for many advanced theories.
The concept of divisibility is not only confined to positive integers. Negative integers can also be even. For instance, -2, -4, -6, etc., are all even numbers because they, too, are divisible by two without a remainder. This universality of the evenness rule is what leads us to consider zero under the same principle.
Why is Divisibility Important?
Divisibility is a critical aspect of number theory as it helps in understanding relationships between numbers. It assists in simplifying fractions, finding common denominators, and solving complex equations. Recognizing a number's divisibility allows mathematicians to classify numbers into various categories, such as even, odd, prime, and composite, each serving a unique purpose in mathematical analysis.
Properties of Even Numbers
- Even numbers are symmetric around zero on the number line.
- They can be expressed as 2n, where n is an integer.
- Arithmetic operations involving even numbers yield predictable results, such as the sum of two even numbers being even.
Mathematical Properties of Zero
Zero is a unique number with distinct properties that set it apart from all other integers. It is the integer that separates positive numbers from negative ones on the number line. Zero is also considered a neutral element in addition, meaning any number added to zero remains unchanged.
In addition to being an identity element for addition, zero plays a pivotal role in multiplication and division. Multiplying any number by zero results in zero, and zero divided by any non-zero number is zero. However, division by zero is undefined, which is one of the peculiarities that adds to zero's intrigue.
Read also:The Ultimate Guide To Utopia Entertainment A World Of Imagination
Furthermore, zero is an even number, conforming to the definition of evenness as it can be divided by two to yield zero, an integer, without a remainder. This characteristic aligns zero with other even numbers, thereby maintaining consistency in mathematical classifications.
Zero's Role in Algebra
In algebra, zero functions as both a placeholder and a pivot point. It marks the origin in coordinate systems and is used to solve equations, particularly those involving roots and intercepts. The zero-product property states that if the product of two numbers is zero, at least one of the factors must be zero, demonstrating zero's foundational role in algebraic problem-solving.
Zero's Unique Characteristics
- Neutral in addition: a + 0 = a.
- Absorptive in multiplication: a × 0 = 0.
- Dividing zero by a number yields zero, but a number divided by zero is undefined.
Is 0 an Even Number?
The question, "is 0 an even number?" is not only intriguing but crucial to understanding number theory. By definition, an even number is any integer divisible by two with no remainder. Zero, when divided by two, results in zero, a whole number, aligning it perfectly with the definition of evenness.
Despite its straightforwardness, the classification of zero as even sometimes perplexes people, primarily because zero's attributes are often misunderstood. However, mathematically, zero satisfies all criteria for even numbers:
- Zero divided by two equals zero, with a remainder of zero.
- Zero can be expressed in the form 2n, where n is an integer (specifically, n = 0).
- Zero fits seamlessly into the sequence of even numbers (… -4, -2, 0, 2, 4 …).
The argument against zero being odd is even more straightforward. Odd numbers, by definition, are not divisible by two without a remainder. Zero clearly does not meet this criterion, reinforcing its classification as an even number.
Mathematical Proofs and Logic
Various mathematical proofs reinforce zero's status as an even number. One such proof involves modular arithmetic, where a number n is even if n mod 2 equals zero. For zero, 0 mod 2 is indeed zero, confirming its evenness.
Another logical approach involves parity, which refers to whether a number is even or odd. Parity remains consistent across arithmetic operations, and since zero is the result of subtracting two equal odd numbers (e.g., 1 - 1 = 0), it retains even parity.
Historical Perspective on Zero
Zero's journey to acceptance in mathematics has been long and complex. Historically, many ancient civilizations did not recognize zero as a number. It was the ancient Indians who first conceptualized zero, around the 5th century, as both a numeral and a placeholder.
The introduction of zero into the number system revolutionized mathematics. It made calculations simpler and more efficient, especially with the advent of the decimal system. Arab mathematicians, like Al-Khwarizmi, further developed the concept, leading to its widespread adoption in Europe during the Middle Ages.
Despite its initial resistance, zero's role in mathematics became undeniable. Its acceptance paved the way for advanced mathematical theories and laid the groundwork for modern computation and algebra.
The Evolution of Zero's Status
Initially, zero was met with skepticism and resistance, partly due to philosophical and theological reasons. Many feared that acknowledging zero would imply the existence of nothingness. However, as mathematical understanding evolved, zero gained recognition for its practicality and indispensability in calculations.
Zero's Impact on Mathematics
- Enabled the development of the decimal system.
- Facilitated the creation of algebra and calculus.
- Led to the formulation of complex numbers and modern computational methods.
Real-World Applications of Zero
Zero's influence extends far beyond theoretical mathematics; it plays a crucial role in everyday life and various fields. From computer science to engineering, zero is integral to numerous applications and technologies.
In computing, binary code, the language of computers, relies on zeros and ones. Zero represents an "off" state, while one signifies "on." This binary system forms the foundation of all digital communication and information processing.
In engineering, zero is vital for calibrating instruments and systems. It serves as a reference point in measuring scales, ensuring precision and accuracy. Without zero, maintaining equilibrium in mechanical systems would be challenging.
Zero's Role in Economics
Economically, zero has significant implications. It forms the basis of zero-based budgeting, a financial method where every expense must be justified for each period. This approach promotes efficient resource allocation and cost management.
Zero's Influence in Science
- In physics, zero is crucial in defining temperature scales, such as absolute zero in Kelvin.
- In chemistry, zero denotes neutral charge in atomic structures.
- In biology, zero can represent baseline measures for growth or decay rates.
Common Misconceptions About Zero
Despite its mathematical significance, zero is often misunderstood, leading to misconceptions that can cloud judgment and reasoning. One prevalent misconception is that zero is neither positive nor negative, making it difficult to categorize.
Another common misunderstanding is that zero cannot be even since it does not have a "pair" like other even numbers. However, this ignores the mathematical definition of evenness based solely on divisibility by two.
These misconceptions often arise from a lack of understanding of zero's properties and its unique role within the number system. Addressing these misunderstandings requires a clear, logical explanation of zero's characteristics and its mathematical basis.
Debunking Myths About Zero
Myth: Zero is not a real number. Truth: Zero is an integer and a real number, occupying a central position on the number line.
Myth: Zero has no value. Truth: Zero has value as a placeholder and is essential in arithmetic operations.
Why These Misconceptions Persist
- Lack of clear education on zero's role in mathematics.
- Cultural and historical biases against the concept of nothingness.
- Confusion arising from zero's unique properties compared to other numbers.
Zero and the Number Line
Zero serves as a pivotal point on the number line, separating positive numbers from negative ones. This central position gives zero a unique role in mathematical operations and number theory.
The number line is a visual representation of numbers arranged in a linear sequence. Zero is positioned at the center, with positive numbers extending to the right and negative numbers to the left. This arrangement highlights zero's role as the boundary between positive and negative integers.
Understanding zero's placement on the number line is crucial for grasping its properties and significance in mathematics. It illustrates zero's function as both a bridge and a barrier, allowing for seamless transitions between positive and negative values.
Zero's Role in Arithmetic Operations
On the number line, zero acts as a reference point for arithmetic operations. It helps in visualizing addition, subtraction, multiplication, and division. This visual aid enhances comprehension and facilitates problem-solving.
Zero's Impact on Geometry
- Zero is used to define coordinates in geometric spaces.
- It serves as a reference for measuring angles and distances.
- Zero is essential for understanding symmetry and balance in geometric shapes.
Teaching Zero as an Even Number
Educating students about zero's status as an even number is vital for building a strong foundation in mathematics. It helps dispel misconceptions and fosters a deeper understanding of number theory.
When teaching zero as an even number, educators should emphasize its divisibility by two and its position within the sequence of even numbers. Visual aids, such as number lines and diagrams, can aid in illustrating these concepts effectively.
Incorporating zero into arithmetic exercises and problem-solving activities can further reinforce its even properties. By presenting zero in various contexts, students can develop a comprehensive understanding of its role and significance in mathematics.
Strategies for Effective Teaching
Use visual aids to demonstrate zero's evenness.
Incorporate real-world examples to illustrate zero's applications.
Common Challenges and Solutions
- Challenge: Students may struggle with understanding zero's unique properties.
- Solution: Provide clear explanations and reinforce concepts through practice and repetition.
How Does Zero Affect Computations?
Zero plays a pivotal role in computations, impacting various mathematical operations and algorithms. Its unique properties can simplify or complicate calculations, depending on the context.
In arithmetic, zero serves as an identity element for addition and a nullifying factor in multiplication. These properties make zero a powerful tool for simplifying expressions and equations.
However, zero can also pose challenges in computations, particularly when it comes to division. Dividing by zero is undefined and can lead to errors in calculations. Understanding these nuances is essential for accurately performing mathematical operations.
Zero's Impact on Algebraic Expressions
In algebra, zero is used to solve equations and find roots. The zero-product property allows for the determination of solutions by setting factors equal to zero.
Zero in Computational Algorithms
- Zero is used to initialize variables in algorithms and programming.
- It serves as a base case in recursive functions and iterative processes.
- Zero is crucial for error handling and exception management in software development.
Zero in Different Mathematical Systems
Zero's role and representation can vary across different mathematical systems and cultures. While its fundamental properties remain consistent, its application and significance may differ.
In the decimal system, zero serves as a placeholder and is essential for representing large numbers. In binary code, zero is one of the two fundamental digits, forming the basis of digital communication.
Other mathematical systems, such as hexadecimal and octal, also incorporate zero, highlighting its versatility and adaptability. Understanding zero's role in these systems provides insight into its universal importance in mathematics.
Zero in Ancient Number Systems
Historically, zero's representation varied across cultures. Ancient Egyptians and Romans did not have a numeral for zero, while the Mayans used a shell symbol to denote zero in their vigesimal system.
Modern Applications of Zero
- Zero is used in scientific notation to express large and small numbers efficiently.
- In computer graphics, zero represents transparency or absence of color.
- Zero is essential in statistical analysis for calculating averages and standard deviations.
Why Does It Matter if 0 Is Even?
The classification of zero as an even number holds significant implications for mathematics and its applications. Understanding zero's evenness helps maintain consistency and accuracy in mathematical analysis.
Recognizing zero as even allows for seamless integration into number sequences and patterns. It ensures that mathematical operations involving zero adhere to established rules and principles.
Furthermore, acknowledging zero's even status reinforces logical reasoning and problem-solving skills. It encourages critical thinking and promotes a deeper understanding of mathematical concepts.
Implications for Mathematical Theories
Zero's evenness supports the development of advanced mathematical theories and models. It plays a crucial role in number theory, algebra, and calculus.
Practical Benefits of Understanding Zero
- Enhances computational accuracy and efficiency.
- Facilitates the development of algorithms and software applications.
- Promotes logical reasoning and critical thinking skills.
Zero in Popular Culture
Zero's influence extends beyond mathematics, permeating various aspects of popular culture. It appears in literature, art, music, and media, symbolizing concepts such as nothingness, infinity, and potential.
In literature, zero is often used metaphorically to represent emptiness or absence. It appears in works ranging from ancient philosophical texts to modern novels and poetry.
In music, zero is referenced in song lyrics and album titles, often conveying themes of introspection and existentialism. Artists use zero to explore ideas of identity, purpose, and the unknown.
Zero in Visual Arts
Zero is a recurring motif in visual arts, representing symmetry, balance, and void. Artists use zero to create thought-provoking pieces that challenge perception and interpretation.
Zero's Role in Film and Media
- Zero is featured in film titles and narratives, symbolizing new beginnings or the unknown.
- In media, zero is used in branding and advertising to convey simplicity and minimalism.
- Zero's representation in digital art highlights its role in modern technology and communication.
Frequently Asked Questions
1. What is an even number?
An even number is any integer divisible by two without a remainder. Examples include 2, 4, 6, and 0.
2. Why is zero considered an even number?
Zero is considered even because it can be divided by two with a remainder of zero, meeting the definition of evenness.
3. Can zero be classified as odd?
No, zero cannot be classified as odd because it does not meet the criteria of being indivisible by two without a remainder.
4. How is zero used in computing?
In computing, zero is used in binary code, representing an "off" state. It forms the basis of digital communication and information processing.
5. What are some misconceptions about zero?
Common misconceptions about zero include the belief that it is not a real number or that it has no value. These misunderstandings arise from a lack of understanding of zero's properties and significance.
6. How does zero impact mathematical operations?
Zero impacts mathematical operations by serving as an identity element in addition and a nullifying factor in multiplication. It plays a crucial role in computations and problem-solving.
Conclusion
In conclusion, zero's classification as an even number is a fundamental aspect of mathematics, supported by logical reasoning and mathematical proofs. Understanding zero's properties and significance is essential for accurate analysis and problem-solving.
Zero's influence extends beyond mathematics, impacting various fields and aspects of everyday life. Its role in computing, engineering, economics, and popular culture highlights its universal importance and versatility.
By recognizing zero as an even number, we maintain consistency and accuracy in mathematical operations and models. This understanding fosters critical thinking, logical reasoning, and a deeper appreciation for the intricate world of numbers.